developed with GRASS
University of Illinois at Urbana-Champaign
Formulation of interpolation problem.
Multidimensional spatial interpolation provides methods for trasformation of values representing landscape phenomena measured at scattered points to 2D, 3D and 4D grids which are suitable for modeling and visualization. This document includes images and animations describing some aspects of spatial interpolation along with numerous application examples. For more detailed description of methods, see publications.
Table 1. Examples of scattered point data transformations to 2D, 3D and 4D grids and visualization of landscape phenomena using point symbols, dynamic surfaces and isosurfaces. Click on the image to retrieve a full size picture (approx. size 50-150K), or animation (approx. size 50-200K)
Visualization of landscape characterization data as multi-variate fields modeled by bi-, tri-, and quad-variate Regularized Spline with Tension |
||||
| phenomenon (field) | point data | 3D dynamic map | ||
|---|---|---|---|---|
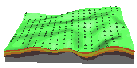
| elevation: z=f(x,y) |  |
 |
||
| precipitation: pi=fi(x,y); i=1,...,12 |  |
mpeg animated gif |
||
| soil horizons: mzi=fi(x,y); i=1,...,5 |  |
animated gif |
||
| soil texture: P=f(x,y,z), P={Sd}, d=20, 80, ... | 
|
 |
||
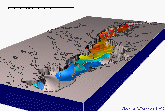
| underground concentrations of chemicals: w=f(x,y,z,t) | 
mpeg animated gif |
mpeg animated gif |
||
| concentration of chemicals in water: w=f(x,y,z,t) |  |
mpeg animated gif |
||
Mitas, L., Mitasova, H., 1999, Spatial Interpolation. In: P.Longley, M.F. Goodchild, D.J. Maguire, D.W.Rhind (Eds.), Geographical Information Systems: Principles, Techniques, Management and Applications, Wiley.
Abstract
This chapter formulates the problem of spatial interpolation from scattered data as a method for prediction and representation of multi-variate fields. The role and specific issues of interpolation for GIS applications are discussed and methods based on locality, geostatistical and variational concepts are described. Properties of interpolation methods are illustrated by examples of 2D, 3D and 4D interpolations of elevation, precipitation, and chemical concentrations data. Future directions focus on a robust data analysis with automatic choice of spatially variable interpolation parameters, and model or process-based interpolation.
Illustrations
Interpolation of elevation surface using different methods available
in GIS:
Fig.1a Voronoi diagram
Fig.1b TIN
Fig.1c IDW
Fig.1d Kriging
Fig.1e Topogrid
Fig.1f s.surf.tps/s.surf.rst , see(RST
method)
Impact of interpolation on results of erosion/deposition modeling:
Fig.2a
Fig.2b
Fig.2c
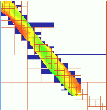
Interpolation of a large DEM using segmented processing:
Fig.3
Fig.3inset
Fig.3leg
Animation of interpolation of a masked river bathymetry using segmented processing:
Animation
Method used
Interpolation of rainfall data without and with incorporation of terrain
influence:
Fig.4a
Fig.4b
the imapct of terrain can tuned using tension anisotropy in vertical direction
animated gif
mpeg movie
Regularized spline with tension: impact of tension parameter in 2D and
3D:
Fig.5a gif
Fig.5b
Fig.5c
Fig.5d
Fig.5e
Fig.5f
Snapshot from quad-variate interpolation of chemical concentrations
data:
Fig.6
The interpolation method implemented in s.surf.tps is regularized spline with tension and smoothing. Tension and smoothing parameters allow the user to tune the character of interpolation to best represent the modeled phenomenon. These two animations show how changing tension and smoothing parameters influence the resulting character of a modeled surface.
(movie - 176,220 bytes)
With increasing smoothing, the surface goes to the trend. Data points lie above and below the interpolated surface.
(movie - 149,235 bytes)
With smoothing set to zero, surface always passes through the original data points. By changing the tension the behavior of the resulting surface changes from thin plate to membrane.
Resampling of Digital Elevation Model
(movie - 30,023 bytes)
Another application of surface interpolation is demonstrated by this animation showing a digital elevation model (DEM) that was patched together at two different resolutions using the standard resampling technique implemented in GRASS. The animation shows how spline can be used for resampling the DEMs without the artificial "steps" caused by standard resampling procedure.
More applications from CERL, GMSLAB and others: (links in preparation)
For a study on modeling of surfaces with faults using splines in GRASS see Toward a Fission Track Tectonic Image of Australia: Model based interpolation in the Snowy Mountains using a GIS by Simon Cox.
Images and animations of surfaces in this document were created using GRASS4.1 program SG3d. Programming, computations and visualization for this project was done by Environmental modeling and visualization group at U.S.Army CERL in 1993 (H. Mitasova, W. Brown, D.P. Gerdes, T. Baker, I. Kosinovsky), interpolation methods were designed by Lubos Mitas from NCSA
Trivariate interpolation transforms scattered data measured in 3D space to a 3D grid and allows us to create volume models of measured phenomena. The tension and smoothing works in a similar way as for 2D:
- movie 3D tension
The applications:
GMSL Modeling & Visualization
