|
|
|||||
|
Using
Soil Erosion Modeling for Improved Conservation Planning: |
|||||
|
|
|||||
|
Using
Soil Erosion Modeling for Improved Conservation Planning: |
|||||
E = R K L S C P
where E [ton/(acre.year)] is the average soil loss, R [hundreds of ft.tonsf.in/acre.hr.year] (in SI: [MJ.mm/ha.hr.year ], R[SI]=17.02R[EU]) is the rainfall intensity factor, K [tons per acre per unit R] = [tons.acre.hr/hundreds.acre.ft.tonsf.in] is the soil factor, LS [dimensionless] is the topographic (length-slope) factor, C [dimensionless] is the cover factor and P[dimensionless] is the prevention practices factor. Various modifications of this equation are often applied to the estimation of soil loss using GIS (e.g., Warren et al. 1989). Revised USLE - RUSLE uses the same empirical principles as USLE, however it includes numerous improvements, such as monthly factors, incorporation of the influence of profile convexity/concavity using segmentation of irregular slopes, and improved empirical equations for the computation of LS factor (Foster and Wischmeier1974, Renard et al. 1991).
LS factor modified for complex terrain
To incorporate the impact of flow convergence,
the hillslope length factor was replaced by upslope contributing area A
(Moore and Burch 1986, Mitasova et al. 1995, 1996, Desmet and Govers 1996).
The modified equation for computation of the LS factor in finite
difference form in a grid cell representing a hillslope segment
was derived by Desmet and Govers (1996). A simpler, continuous form of the equation for computation of the LS factor at a point r=(x,y)
on a hillslope, (Mitasova et. al. 1996) is
LS(r) = (m+1) [ A(r) / a0 ]m [ sin b(r) / b0 ]n
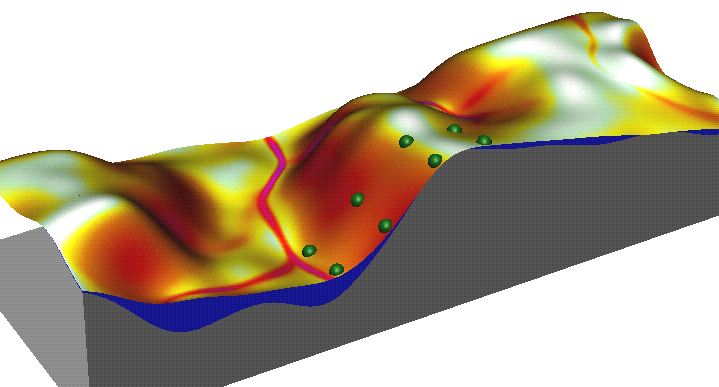
where A[m] is upslope contributing area per unit contour width, b [deg] is the slope, m and n are parameters, and a0 = 22.1m = 72.6ft is the length and b0 = 0.09 = 9% = 5.16deg is the slope of the standard USLE plot. The impact of replacing the slope length by upslope area on the detachment pattern is illustrated by the following figures, which show that the upslope area-based factor better reflects the impact of concentrated flow on increased erosion:
Length-based LS
Upslope area based LS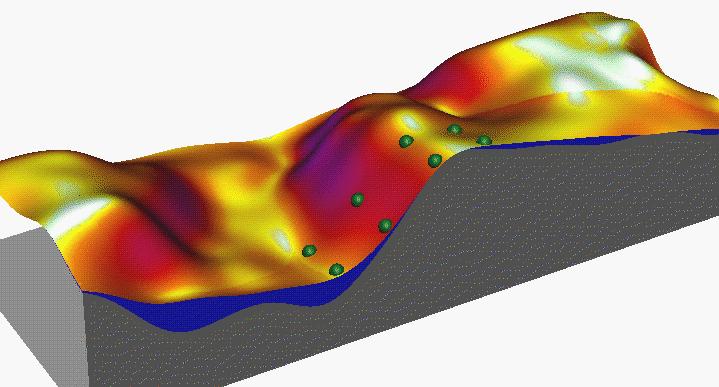
Choosing exponent parameters
The typical values for
m and n are 0.4-0.6 and n=1.0-1.4 depending on the
prevailing type of flow (higher values are for more rilling).
Exponents
m and n can be calibrated if data are available
for a specific prevailing type of flow and soil conditions. Lower values for m and
n should be used for areas with prevailing dispersed flow, such as areas well covered with vegetation. Higher values should be used for areas with a more turbulent type of flow caused by existing rills or disturbed areas.
In this tutorial we consider the exponents constant for the entire study area, so for example, we would use
m=0.4 and n=1 for the Owl Creek watershed at Fort Hood which has mostly natural vegetation, while
m=0.6, n=1.3 would be more appropriate for the House Creek watershed with mostly disturbed areas susceptible to rilling
and gullies. RUSLE also
includes an equation for variable m which is a function of slope
steepness and Nearing et al. have derived a new equation
for the slope factor. Both can be used instead of the simpler
equation presented here.
Application
of RUSLE
Both the standard and modified equations
can be properly applied only
to areas experiencing net erosion. Depositional areas should
be excluded from the study area because the model assumes that transport
capacity exceeds detachment capacity everywhere and erosion and sediment
transport is detachment capacity limited.
Therefore, direct application of USLE/RUSLE to complex terrain within
GIS is rather restricted. The results
can also be interpreted as an extreme case with maximum possible spatial extent
of erosion.
|
|
HOME