Terrain modeling and Soil Erosion Simulations for Fort Hood and Fort Polk test areas

 
 
 
 
 
 
 

Prepared by:

Geographic Modeling and Systems Laboratory, University of Illinois at Urbana-Champaign

Helena Mitasova, Lubos Mitas, William M. Brown, Douglas M. Johnston

 

for :

U.S. Army Construction Engineering Research Laboratories
Dr. Dick Gebhart

 
 
 
 
 
 
 
 
 
 
 
 
Annual Report
1999

 
 
 
 
 
 

Content


 
  

1. Introduction.............................................3

2. Methods..................................................4

   2.1 Input data processing................................5

   2.2 Erosion models.......................................8

       2.2.1 USLE...........................................9

       2.2.2 USPED.........................................10

       2.2.3 Process based simulation of water erosion.....11

   2.3 GIS implementation of models........................14

       2.3.1 GRASS5.0......................................14

       2.3.2 ArcView Spatial Analyst.......................16

3. Applications............................................18

   3.1 Fort Hood subwatershed: comparison with Cs137.......18

   3.2 Fort Polk erosion potential....................21

4. Conclusion and future directions........................22

5. References..............................................23

6. Appendix................................................24

   6.1 Manuals and tutorials

   6.2 Data

   6.3 On-line documents

 
 
 
 
 
 
 
 
 
 
 

1. Introduction

Increasing pressures on the land and an improved understanding of human impacts on the environment lead to profound changes in land management, with emphasis on integration of local actions with watershed-scale approaches. This trend has a significant impact on the development of supporting GIS and modeling tools by creating a need for a wide range of tools at different levels of complexity and realism. There is a growing need for complex, distributed physics-based models which can predict results of landscape processes at any point in space and time at multiple scales, but at the same time the landowners and land managers working in the field need simple, fast and easy to use models for which the input data are readily available.

Research and experience have delivered a rich set of tools and techniques for evaluating and managing soil erosion from various sources within watersheds. While significant gains in the control of soil erosion have been made, there remain significant problems with sedimentation of water supply and navigation systems, transport of soil attached contaminants and the cost of some management techniques. Further, while much research exists for individual methods in individual locations little work has been devoted to integrated approaches which characterize interaction between erosion processes and management methods across scales and within a system of land management strategies

To better support the multilevel management we propose a methodology for watershed characterization and erosion modeling at multiple scales and levels of complexity. Because the spatial unit, modeled at the local level is a part of a larger watershed, the evaluation of the impact of numerous, locally implemented conservation practices on the entire watershed requires multiscale approach which links the high resolution, local level simulation with low resolution/regional simulation. Models and simulations of watershed behavior demonstrating how the lands within the watershed are connected, how they interact and influence each other help to better understand the impact of local actions within the watershed necessary for successful conservation and sustainable land management programs.

Recent advances in Geographic Information Systems (GIS) technology, linkage of numerous models with GIS, (Moore et al. 1993, Saghafian et al. 1995, Srinivasan and Arnold 1995) create a potential to develop an environment for coordination of conservation efforts at a hierarchical system of management levels by providing the tools to design and evaluate the impact of land use alternatives at both local and watershed/regional levels for a given time horizon.  They facilitate evaluation of prevention practices not just depending on the type of the prevention measure, but also on their location within the watershed. Spatial analysis and simulations can also provide supporting information for allocation of resources to those areas and those types of practices which will provide the most effective protection. Distributed models facilitating multiscale approach have been recently identified as promising for studies of landscapes with significant human impact, such as agricultural and urbanized watersheds. However advances in models, algorithms and GIS tools are needed to fully support this approach.

Simulation modeling which can give decision makers interactive tools for both understanding the physical system and judging how management actions might affect that system was identified in a report "New Strategies for America's Watersheds" (Committee on Watershed Management, National Research Council 1999) as one area of special promise for watershed management. This report analyzes the current status in watershed modeling for decision making and concludes that the available models and methods are outdated and "a major modeling effort is needed to develop and implement state-of-the-art models for watershed evaluations"(pp.160-161). The development of distributed models supported by SERDP and this project is one step in the direction identified in the report as crucial for the land use management in America's Watersheds.
 

2. Methods

Effective conservation of natural resources involves planning and decision making at different scales and levels of detail (Figure 1). At a regional scale, watersheds are often represented as homogeneous units with terrain, soil, and cover conditions described by averaged values. The watershed based models (e.g., SWAT: Arnold et al. 1993) simulate a broad spectrum of processes (surface and subsurface water flow, sediment and pollutant transport, etc.) with continuous time simulation. The results represent averages for entire watersheds/subwatersheds, so lower resolution (100-30m) raster or polygon data are sufficient. This approach supports management at a regional, level, which involves, for example, identification of watersheds with high risk composition of land use, or designation of watershed level conservation areas.

Local level of management requires detailed spatial representation (10-1m resolution) and models capable to simulate effects of spatially variable land cover. This level of detail is necessary for implementation of conservation practices at the most effective locations, as well as for selecting the projects that save the most soil or benefit the most acres per dollar cost. The empirical models such as USLE/RUSLE, which have been used at this level for many years, are now being replaced by process-based models, such as WEPP (Flanagan and Nearing 1995). Both RUSLE and WEPP are based on routing of water and sediment over hillslope segments and pre-defined channels, a concept which requires substantial manual input and is not very practical for large areas typical for military installations.

New generation of models based on raster representation of multivariate functions has been developed recently with the support from SERDP and ARO (SIMWE: Mitas and Mitasova 1998, CASC2d: Julien, Ogden, Saghafian, Johnson 1995-99, MIT models: Brass, Willgoose, Moglen, SIBERIA, CHILD 1992-1998)). These models have a potential, after undergoing a substantial experimental testing and calibration, to be useful for both local and a regional scale modeling.

Figure 1. Modeling at different levels

The watershed models based on homogeneous spatial units have been described in detail in literature (e.g., Arnold et al. 1993) and are widely available, including the possibility to run the model online. Therefore, we focus on distributed modeling of erosion and deposition patterns for spatially variable conditions. Within the spatially continuous approach, model inputs and outputs are represented by multivariate functions discretized as grids. Flows of water and sediment are described as bivariate vector fields rather than commonly used systems of 1D flows (e.g., Moore et al., 1993). To support modeling at different levels of complexity we have developed a set of tools which range from modifications of relatively simple empirical models to a more complex, process-based approach. GIS technology is used to support the processing, analysis and visualization of the data and simulation results (Mitas et al., 1997). The models are described in detail in our previous report (Mitasova et al., 1998) therefore in the following sections we focus on the issues related to practical applications of the models and their use with GIS.

2.1 Input data processing

With the growing capabilities to collect digital data about landscape from various sources using different technologies it is common that the data characterizing the studied landscape are very heterogeneous with different coverage, resolution, detail and accuracy (Figure 2.). To fully exploit the data available for given area for modeling algorithms should be able to handle and make effective use of such heterogeneous data sets, maximize the accuracy and detail of predictions while performing computations efficiently.

Figure 2. Diverse set of elevation data available for Hohenfels: 10m DEM from contours, 4m DEM from remote sensing (IFSARE), 2m DEM from detailed contours.

Preparation of data for modeling and land use management still requires a substantial effort, in spite of the great progress in the measurement techniques and distribution of data. While the spatial data are currently much easier to exchange and import/export between different systems, with higher resolutions the data sets are substantially larger and often more complex. The growth of the size of data sets is "keeping up or even exceeding" the growth of computational power and efficient GIS tools for processing, analyzing and visualizing spatial data for land use management are as important as ever. When processing the spatial data, we are focusing on extensive use of standard GIS tools available in both commercial and public license systems, such as GRASS5.0 and ArcView/Spatial Analyst, however enhancements or modifications of existing tools are often needed to fulfill the needs of distributed, process-based modeling.

Spatial interpolation and smoothing is necessary for transformation of scattered data to regular grids, resampling of grid data and smoothing of data with noise. The selection of an adequate method and its parameters can have a profound impact on the predicted patterns, as we have shown e.g. in Mitas and Mitasova 1999. The current project has again demonstrated the crucial role of spatial interpolation for processing of DEMs from various sources (ISARE, contours, field measurements) as well as for the interpolation of Cesium data. We have used and enhanced the bivariate regularized spline with tension and smoothing (RST, Mitas and Mitasova 1999) and its implementation in GRASS5.0 to perform spatial interpolation and topographic analysis for this project applications, in particular for smoothing of the IFSARE data (see section 3.1), interpolating field measured elevations with fault, interpolating very large combined point and contour data set and deriving surface gradients for water and erosion models.

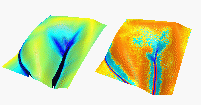
Interpolation of data with a fault by RST. Spline is by definition a smooth function and has always been regarded as a tool for representation of smooth surfaces. Therefore its application to surfaces with faults has been often described as problematic. However, RST combined with GIS masking tools can be very effectively used to create models of surfaces with complex pre-defined faults by using multiple-pass approach similar to zonal kriging. First, the points defining the fault are extracted from the elevation data set based on their attributes and transformed from site through vector to raster masks representing continuous (smooth) subsets of the data. The masks are then used to create separate elevation data subsets for each smooth subregion which is then interpolated by RST. The masked surfaces are then merged using map algebra to create a single surface with faults (Figure 4a)

Figure 3. DEM without the gully fault a), b)

Figure 4. DEM with the gully fault

Surface analysis provides basic topographic or surface geometry parameters needed for modeling of fluxes in landscape, including water and sediment. Estimation of slope and aspect (direction of flow) are standard functions in GIS software and their computation using the RST methods is described by Mitasova and Hofierka 1993. For several hydrologic and erosion models which simulate water and sediment flow as a bivariate function, partial derivatives dz/dx, dz/dy representing the surface gradient grad z, are needed:

grad z =(dz/dx,dz/dz)         (1)

We have used two approaches to estimate partial derivatives. First is based on a local polynomial approximation of a surface at a grid point from the elevations in its 3x3 neighborhood (Shapiro and Westervelt 1992). This approach can be applied only to raster data and has been implemented as an option for the command r.slope.aspect in GRASS5.0. It can also be implemented using map algebra functions as shown e.g. by Shapiro and Westervelt 1992. The second approach is based on the derivatives of the RST function (Mitasova and Hofierka 1993) and it can be used for both scattered points and raster data. This approach is implemented as an option for the s.surf.rst command in GRASS 5.0. To compute the partial derivatives within a GIS where the direct computation of derivatives is not available we use the known relationship between the slope b and aspect a angles and the partial derivatives of the function z:

dz/dx = tg(b).cos(a)         (2)

dz/dy = tg(b).sin (a)         (3)

where b is slope and a is aspect in degrees, computed by standard GIS functions.

Flowtracing for computation of slope length and upslope area is performed by r.flow. The program has undergone some modifications in 1995 to reduce the stripes caused by 1D flow on convex hillslopes where dispersal flow occurs. This modification introduces a small level of noise into the results which can be smoothed out by r.neighbors. Better solution is possible by using multiple direction flow. The problems with dispersal flow have been fully resolved by simulation of flow as a bivariate vector field in SIMWE, however a simple flowtracing implemented as a GIS command is still a useful alternative to full process based simulation.

Terrain modification tools are useful for incorporation of data about streams and rivers into terrain model, which usually captures only the approximate water surface elevation. We have developed a methodology for modification of a DEM by "carving-in" streams and rivers using their vector representation and attributes such as width and depth. The method was implemented as r.enforce in GRASS5.0, an example of terrain model with "carved-in" river is in Figure 5.

Figure 5. DEM with "carved-in" stream

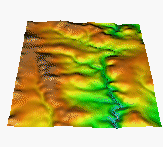
Visualization is an integral part of input data processing as well as of communication of  the results. After porting the underlying libraries to OPEN GL at GMSLab (Brown 1998) and as a result of collaboration with a research group in Europe, the 3D surface visualization tool NVIZ2.2 is now available for PC under LINUX and for SUN workstations within the new  GRASS5.0 release. The capability to visualize multiple surfaces has been invaluable in the development of erosion models.

New visualization tools were developed for tracking the computation progress during interpolation of very large DEMs (millions of cells from hundreds of thousands of points) using the RST method, which often takes several hours even on fast, state of the art computers.

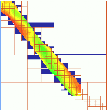
Figure 6. Real time tracing of computation by RST

We have renewed our use of p.vrml which allows us to directly serve the results as 3D interactive models on the Internet. While most of the VRML viewers are not well designed for exploration of geospatial data, their speed and convenience has improved sufficiently for practical use.

Figure 7. VRML model of FT. Hood subwatershed

2.2 Erosion models

To support land use management at various levels we have designed approaches for a set of GIS-based erosion models with increasing complexity (Figure 8). The simple models are based on well established empirical equations with data  readily available, however, their applicability to wide range of conditions and phenomena is limited. The  new distributed, process-based models allow us to simulate more complex effects, however, both the experimental and theoretical research aspects are still very active and underlying equations as well as the input parameters are under continuing development. The distributed approach to modeling which allows us to predict the impact of processes on landscape patterns revealed substantial gaps in theory of erosion processes in complex landscapes and spatially distributed field experiments integrated with modeling is needed to improve our understanding of complex interactions involved in erosion processes and bring the quantitative accuracy of predictions (which is currently at about 50-150%) to acceptable and useful levels.

Figure 8. Erosion models

2.2.1 Universal Soil Loss Equation

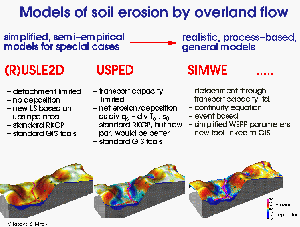
The Universal Soil Loss Equation (USLE) is a well known empirical equation developed for simple, field-based estimates of average annual soil loss using factors derived from a very large experimental data set:

E = R K L S C P         (4)

where E [ton/(acre.year)] is the average soil loss, R [hundreds of ft.tonsf.in/acre.hr.year] (in SI: [MJ.mm/ha.hr.year ], R[SI]=17.02R[EU] or [N/h=kg m/s3]) is the rainfall intensity factor, K [tons per acre per unit R] = [tons.acre.hr/hundreds.acre.ft.tonsf.in] is the soil factor, LS [dimensionless] is the topographic (length-slope) factor, C [dimensionless] is the cover factor and P[dimensionless] is the prevention practices factor. Several approaches were developed to adapt this field based model to GIS use. R,K,C and P factors are usually derived from land use and soil maps (digitized or derived from imagery), and slope and slope length for the LS-factor are derived from a DEM. While GIS has relatively good tools for estimating slopes, deriving a slope-length map is more problematic.   Examples of L-factor estimation and implementation include use of (i) average slope length for the entire area, (ii) average slope length for each soil type, (iii) spatially variable slope length estimated for each cell from a DEM using a flowtracing program such as r.flow in GRASS (Mitasova and Hofierka 1993, Figure 9, Appendix). The LS factor is then computed as

LS=(l/22.13)0.6 . [65.4.(sin b) 2 + 4.56sin b + 0.0654]       (5)

where l[m] is the slope length and b[deg] is the slope angle.

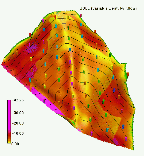
Figure 9. USLE with different LS factors: a)average length, b)distributed length, c)upslope area

To incorporate the impact of flow convergence, a replacement of the slope length by the upslope contributing area per unit contour width was suggested, e.g., by Moore and Wilson 1992, Mitasova et al. 1996, Desmet and Govers 1996. The modified LS factor at a point on a hillslope is

LS = (m+1) [A / 22.13]m [sin b  / 0.0896]n                                 (6)

where A[m] is upslope contributing area per unit width, b[deg] is the  slope angle,  m and n are parameters. Exponents m and n should be calibrated for a specific prevailing type of flow and soil conditions, if the data are available. Moore and Wilson (1992) have shown that the values of m=0.6, n=1.3 give results consistent with RUSLE LS factor for the slope lengths <100m and the slope angles <14 deg for slopes with negligible tangential curvature. We use the equation (6) as an approximate LS factor for estimation of soil loss using RUSLE, with the assumption that transport capacity exceeds detachment capacity everywhere, erosion and sediment transport is detachment capacity limited and therefore no deposition occurs. Impact of replacing the slope length by upslope area is illustrated in Figure 9, which shows that the upslope area better describes the increased erosion in the areas of concentrated flow and allows to identify areas with potential for gully erosion. More research is needed to quantitatively determine the erosion rates in these areas as the type of flow changes dramatically and different equations or at least parameters are needed to estimate the erosion rates by concentrated flow.

Both the standard and modified equations can be properly applied only to areas experiencing net erosion. Deposition areas should be excluded from the study area because the model assumes that  transport capacity exceeds detachment capacity everywhere and erosion and sediment transport is detachment capacity limited. Therefore, direct application of USLE/RUSLE to complex terrain within GIS is rather restricted. The results can also be interpreted as an extreme case with maximum spatial extent of erosion possible.
 

 2.2.2 Unit Stream Power based Erosion/Deposition model

USPED (Unit Stream Power - based Erosion Deposition) is a simple model which predicts the spatial distribution of erosion and deposition rates for a steady state overland flow with uniform rainfall excess conditions for transport capacity limited case of erosion process. The model is based on the theory originally outlined by Moore and Burch 1986 with numerous improvements. For this case, we assume that the sediment flow rate qs[kg/ms]? is at the sediment transport capacity T[kg/ms], (Julien and Simons 1985)

|qs|  =  T  =  Kt |q |m [ sin b ]n      (7)

where q[m2/s] is the water flow, Kt[kg/m3] is the soil transportability coefficient, m, n are constants dependent on the type of flow and soil properties. Steady state water flow can be approximated as a function of upslope contributing area |q | = A i, where i[m/s] is rainfall intensity. All units are for m=1.

No experimental work was performed to develop parameters needed for USPED, therefore we use the USLE or RUSLE parameters to incorporate the impact of soil and cover to obtain at least a relative estimate of net erosion and deposition.We assume that we can estimate sediment flow at sediment transport capacity as

 T = R K C P Am (sin b)n          (8)

where R ~ i m[N/h=kg m/s3=c1*m/s, c1=kg/s2], KCP ~ Kt[kg/m3]    and LS=Am sin b n [m] (in this case LS includes impact of both the topography and amount of water through A). Then the net erosion/deposition is estimated as

ED  =  div (T . s)  =  d(T*cos a)/dx  +  d(T*sin a)/dy          (9)

where s is a unit vector in the flow direction, a [deg] is aspect of the terrain surface.This equation is equivalent to the relationship with curvatures presented in the report by Mitasova et al. 1998, however, the computational procedure is simpler.   The exponents m and n control the relative impact of water and slope terms and reflect different erosion patterns for different types of flow. The exponents theoretically consistent with the RUSLE  are m=1.6, n=1.3 and they seem to reflect pattern for prevailing rill erosion (net erosion is computed as a derivative of T, which leads to an exponent 0.6 used in USLE) with erosion sharply increasing with the amount of water (Figure 10a). The observed extent of colluvial deposits in our previous study indicated lower exponents reflecting compound, long term impact of rill and sheet erosion and both large and small events. The exponents m=n=1 predict greater spatial extent of deposition suggesting prevailing sheet erosion (Figure 10b). Comparison with SIMWE simulations shows that m<1 leads to pattern with small erosion/deposition rates but large spatial extent of deposition a situation which may occur during a small event.

Figure 10. Impact of exponent m on the erosion/deposition pattern: a) m=1.6 prevailing rill erosion, b) m=1 prevailing sheet erosion , c)m=0.6 small event. The results for m<=1 are multiplied by 10 and 100 to compensate for the smaller exponent and to make the values easier to compare.

Caution should be used when interpreting the results because the USLE parameters were developed for simple plane fields and detachment limited erosion therefore to obtain accurate quantitative predictions for complex terrain conditions they need to be re-calibrated ( Foster 1990, Mitasova et al 1997 reply).

2.2.3 Process-based simulation of water erosion

The new generation erosion model SIMulation of Water Erosion model (SIMWE) is based upon the description of water flow and sediment transport by first principles equations (e.g., Foster and Meyer 1972, Bennet 1974) with the core theoretical principles based on the WEPP (Flanagan and Nearing 1995). The model is described by Mitas and Mitasova (1998) and in our previous reports, therefore we briefly present only its principles and recent enhancements. The steady state version SIMWE1.0 estimates the net erosion/deposition D(r) at a point r=(x,y) as a divergence of a vector field q(r) representing sediment flow:

D(r) = div q(r),
(10)
under the assumption that the erosion and deposition are proportional to the difference between the sediment transport capacity T(r) and the actual sediment flow rate q(r) (Foster and Meyer, 1972):

D(r) = C(r)[T(r)-|q(r)|]
(11)
where C(r) is the first order reaction coefficient dependent on soil and cover properties. We solve the continuity equation in a modified form:

-(1/2)d nabla2 p(r) + div [p(r) v(r)] + p(r)C(r)|v(r)| = C(r) T(r)
(12)
where p(r) =|q(r)|/|v(r)|, v(r) is the water flow velocity, and d is the diffusion constant. The equation (12) is solved by a stochastic method which provides the robustness necessary for handling rapid changes in input fields, especially in land cover, often caused by human intervention. Results of the model depend on the interaction between the input fields, especially the soil transport and detachment capacities and actual sediment loads and detachment rates.

The model is being continually enhanced by including more complete and more general description of the simulated processes. The following enhancements were useful for the applications in this project:

While our previous efforts focused on hillslope water flow and erosion these enhancements are a step towards modeling the interaction between channels and overland flow, an important and not very well understood phenomenon. Flat areas or depressions are often drained by natural or manmade channels which are given as vector data and usually are not represented in the DEMs. Flat areas and depressions without channels can hold substantial amounts of water and are often suitable for wetlands - one of important and popular land management practices. SIMWE was therefore enhanced to simulate the flow in flat areas either as a shallow diffusive flow creating wet areas with standing water or as a flow through predefined channels given by stream/channel network.

Figure 11. Water depth pattern in flat areas a) without stream/channel, b)with streams/channels with average 2 deg slope.

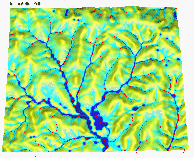
We are also moving beyond the steady state modeling by introduction of real time and simulation of events with a given time period. This allows us to predict erosion/deposition patterns for small events when water flow has not reached the steady state, as illustrated by the following example of a field in Exeter, England, when center of the valley has depositional area for smaller events and gully erosion for large events.

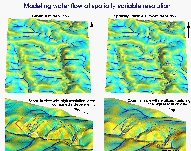
Figure 12 Erosion/deposition pattern for rainfalls with increasing length, leading to gully development

The necessity for spatially heterogeneous modeling of fluxes can arise due to various reasons:
(a) study area is represented by data with spatially variable resolution and accuracy  (study area has high resolution data however there is mass coming in from an area for which we have only low resolution data);
(b) study area is large, with spatially variable complexity for which simulation with spatially variable precision or detail is the most effective (study area is large, but a certain part of it is homogeneous so it is unnecessary to run it all at high resolution, only area of interest/highs spatial variability will be simulated at high resolution while the rest is low resolution.)
The system of continuity equations used in SIMWE describes the water and sediment flow at a spatial scale equal or larger than an average distance between rills (i.e., grid cell size more than 1m) and therefore the presented approach allows us to perform landscape scale simulations at variable spatial resolutions from one to hundreds of meters, depending on the complexity and importance of studied subregions. The solution of continuity equations through the Green's function can be reformulated for accommodation of spatially variable accuracy and resolution  by introducing a weighting function. This weighting function can change (abruptly or smoothly)  between regions with unequal  resolutions and in fact, can be optimally adapted to the quality of  input data (terrain, soils, etc.) so that the accurate solution  is calculated only in the regions with correspondingly accurate inputs.  The reweighted Green's function in effect,  introduces higher density of sampling points in the region with  large weight. The statistical noise will be spatially  variable as  a function of the average number of samples  resulting in the accuracy increase for the areas  with weight function > 1.

Figure 13. Multiscale water flow

2.3 GIS implementation of models

Simple models use standard data structures (raster) and commonly available  GIS tools to limit the need for code maintenance and ensure simplicity of use. We present the implementation at a command line level to keep the implementation as general as possible and allow easy implementation in different land use management or modeling environments using specific GUI, including web based implementation for on-line spatial erosion/deposition computational tools. The tutorials which include the links to manual pages as well as images are in the online Appendix.

We have tested implementation in 2 systems :

The efficient use of the models requires full floating point support and nonlinear categorization and color tables capabilities. It is possible to run the computations and create the resulting maps without these capabilities, however, tracking the necessary multiplications and difficulties with creating meaningful maps make it very time consuming and prone to errors.

In the following examples we assume that the given data are raster maps representing elevation, K, C, R and optionally also the P factors, and resolution as a constant. The erosion is always negative (including USLE), deposition is positive.

2.3.1. GRASS5.0

USLE
a)using average slope length: simplified example  for 2 soils with different K-factor used for the Ft. Hood application (for more soil types r.average whas been modified to compute the averages from values for each soil r.average.sh base=K cover=length out=length_av )

r.flow -u elevation lgu=length
r.slope.aspect elevation slope=slope aspect=aspect
r.mapcalc

slg1=if(K_mask,length)
slg2=if(K_mask,0,length)
r.sum slg1->  2,816,212 average lg is 140
r.sum slg2 -> 828495  average lg is 69.
r.mapcalc
length_av=if(K_mask,140,69)
usle_lg_av=-R*K*C*1.6*exp(length_av/22.13,0.6)*(65.4*sin(slope)*sin(slope)+4.56*sin(slope)+0.0654)
b)using spatially variable slope length

r.flow -u elevation lgu=length
r.slope.aspect elevation slope=slope aspect=aspect
r.mapcalc

usle_lg=-R*K*C*1.6*exp(length/22.13,0.6)*(65.4*sin(slope)*sin(slope)+4.56*sin(slope)+0.0654)
c) using upslope area instead of slope length

r.flow elevation dsout=flowacc
r.slope.aspect elevation slope=slope aspect=aspect
r.mapcalc

usle_area=-R*K*C*1.6*exp(flowacc*resolution./22.13,0.6)*exp(sin(slope)/0.0896),1.6)
Note: USLE has not been developed for areas with concentrated water flow, therefore the values in those areas often exceed the typical erosion rates for USLE. The higher erosion rates are often realistic as there is a  high potential for gully formation due to the concentrated water flow. However, if the values are too high even for gullies it is necessary to reclass the erosion rates to a reasonable value which can be expected for gullies in the studied area. This reclass procedure affects only a very small number of grid cells and has a little impact on erosion averages for the entire region. Development of suitable parameters for predicting the erosion by concentrated flow will be the focus of a future proposed research.

USPED (can be written as a script)

r.flow elevation dsout=flowacc
r.slope.aspect elevation slope=slope aspect=aspect
r.mapcalc

sflowtopo=exp(flowacc*resolution,1.6)*exp(sin(slope),1.3) (prevailing rills)
or
sflowtopo=flowacc*resolution*sin(slope) (prevailing sheet)
qsx = R * K * C * sflowtopo * cos(aspect)
qsy = R * K * C * sflowtopo * sin(aspect)
r.slope.aspect qsx dx = qsx.dx
r.slope.aspect qsy dy = qsy.dy
r.mapcalc
erdep = qsx.dx + qsy.dy (prevailing rills)
erdep = 10. * (qsx.dx + qsy.dy)  (prevailing sheet)
r.colors erdep rast=color_erdep (color_erdep is a raster file with standardized, non-linear erosion/deposition map colortable)

Note: Similarly as in the case of modified USLE, the model may produce very high erosion in areas of concentrated flow, especially for the prevailing rill erosion. These areas represent only a very small percentage of modeled area and should be reclassed to values typical for gully erosion.

2.3.2 ArcView/Spatial Analyst

There are several aml scripts and other implementations of USLE in the ESRI products or as field based, on-line calculators available over the Internet. We present an implementation for raster data using the standard commands in ArcView with Spatial Analyst extension.

USLE based on upslope area

 select elevation
   under Analysis select DERIVE SLOPE   give the new theme name slope

MAP CALCULATOR
    build an expression
    ([elevation].FlowDirection(FALSE)).FlowAccumulation(NIL)
    Evaluate,  give the new theme name  flowacc

    build an expression :
    (([flowacc] * resolution/22.1).Pow(0.6))* ((([slope]*0.01745).Sin)/0.09).Pow(1.3))*1.6
    Evaluate, give the new theme name lsfac

    build an expression
    -1.*R*[K]*[C]*[P]*[lsfac]
    Evaluate, give the new theme name usle_area

USPED

   select elevation
   DERIVE SLOPE,  name it slope
   DERIVE ASPECT,  name it aspect

MAP CALCULATOR
       build en expression
       ([elevation].FlowDirection(FALSE)).FlowAccumulation(NIL)
       Evaluate, name it flowacc

MAP CALCULATOR
   build an expression (prevailing rill erosion):
    (([flowacc] * resolution).Pow(1.6))* ((([slope]*0.01745).Sin).Pow(1.3))
    Evaluate, name it sflowtopo
  or for prevailing sheet erosion
    ([flowacc] * resolution)* (([slope]*0.01745).Sin)
    Evaluate, name it sflowtopo

Important : the values of K and C should be multiplied by 100 (see note below)
    build an expression
    (((([aspect]*(-1))+450)*0.01745).Cos)*[sflowtopo]*[K]*[C]*R
    Evaluate,  name it qsx
    (((([aspect]*(-1))+450)*0.01745).Sin)*[sflowtopo]*[K]*[C]*R
    Evaluate,  name qsy

   select qsx
   DERIVE SLOPE,   name it qsx.slope
   DERIVE ASPECT,  name it qsx.aspect

   select qsy
   DERIVE SLOPE,  name it qsy.slope
   DERIVE ASPECT,  name it qsx.aspect

 MAP CALCULATOR
       build an expression
       (((([qsx.aspect]*(-1))+450)*0.01745).Cos)*([qsx.slope]*0.01745).Tan
       Evaluate, name it qsx.dx
       build an expression
       (((([qsy.aspect]*(-1))+450)*0.01745).Sin)*([qsy.slope]*0.01745).Tan
       Evaluate, name it qsy.dy
       build an expression
       [qsx.dx] + [qsy.dy]
       Evaluate, name it erdep

It is necessary to keep in mind that the resulting values for erosion and deposition are multiplied by the values used to multiply the C and K factors. Do not divide to get the correct values, because the pattern with values in interval <-1,1>, typical for well preserved areas as well as for the relatively flat areas, will be lost. We were not able to visualize the erosion/deposition map when using the true values of K and C, because ArcView has troubles handling floating point numbers in the interval <-1,1> . According to the Spatial Analyst manual, floating point grid themes can only use equal interval or standard deviation for classification which are unsuitable for erosion/deposition maps. Several examples of problems encountered when computing erosion/deposition maps  with true values of K and C are presented in the online Appendix. It is also important to note that the algorithms available in ARC are different from those in GRASS, therefore to obtain acceptable result more attention should be paid to the proper selection of resolution and to the quality of DEM.

Figure 14. Erosion/deposition from GRASS and Arcview

Because of profound changes in ESRI software which involves merging of ArcINFO and ArcView, release of ArcModel and our troubles with displaying the maps in Arcview3.1,3.2 we propose testing the model again under the new release of ArcInfo8 for which the GMSLab will be a beta tester.

Process-based simulation implemented as SIMWE1.0 is designed as a research tool linked to GRASS and ArcInfo/ArcView through import/export of raster data. Most of preprocessing, visualization and analysis is done within GIS only the simulation of the water flow and sediment flow processes is run by the stand alone program.

The approach used for SIMWE which is based on modeling with multivariate fields and the  Monte Carlo solution of continuity equations opened new possibilities for simulation of a broad range of phenomena related to flow of water and sediment and their interaction with terrain and land cover. Therefore SIMWE is being continuously enhanced and further developed by adding more complete description of modeled processes and modifications reflecting the recent results of experimental research. The proposed multiscale approach can be implemented within any  standard raster GIS without the need for developing new data structures. For each resolution a separate set of inputs is created with overlapping region, simulation algorithm combines the data from different files by going through several passes of computation. Algorithm produces a useful byproduct - identification of borderline segments with inflow of water and sediment and segments with outflow - important for identification of areas which require protection from e.g. inflow of harmful chemicals or areas where outflow of contaminated material should be controlled (Figure 13).

To perform the routine modeling efficiently, a customized interface can be created for particular applications.
 

3. Applications

 3.1 Fort Hood subwatershed: comparison with Cs

The presented erosion models were applied to a small watershed at Fort Hood and the results were compared with the estimates of soil loss using the Cs137 measurements. The Cs measurements and analysis of the results will be described in detail in a separate report by Warren et al. 1999, here we describe the computations and results related to this project.

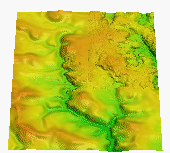
Computation of Digital Elevation Model. We have used 2 different sources of elevation data : a) IFSARE from TEC and b) point data from direct field measurement from the local NRCS. The IFSARE data from TEC were provided as integer values creating artificial steps along 1m contourlines and making the use of data for modeling of water and sediment flow problematic (Figure 15a). Upon our request, we were also provided with the original floating point IFSARE data where the artificial steps were not present and data were more suitable for modeling. However, both data sets contained speckle noise typical for radar data which has to be removed to make the data useful for applications. The noise was relatively homogeneous and appeared as "bumps" about 1-3m high/wide on top of the measured terrain surface with vegetation (Figure 15a,b). In spite of the fact that the RST method has not been designed specifically to deal with the speckle noise, we have found that the RST method performed very well as a smoothing tool allowing us to create usable representation of terrain for the studied watershed (Figure 15c).

Figure 15. DEM from IFSARE data a) integer IFSARE data distributed by TEC, b) original, floating point IFSARE data c) smoothed floating point IFSARE data (data a,b courtesy TEC USACE).

High quality field data were provided by NRCS with coded fault and border lines which allowed us to test the RST method for surface interpolation with fault (Figure 4). The gully was mapped with a substantially higher density of points therefore we will be able to use this data set to test it for multiscale representation of terrain and modeling of flow on the hillslopes and inside the gully. Because of their higher accuracy and detail we present here the results of modeling using the NRCS field data with slightly smoothed gully. The model results for the IFSARE data are in the online Appendix.

Erosion modeling. We have focused on comparison of different approaches based on USLE parameters and we have also run some simulations with SIMWE. The USLE and USPED parameters were determined based on the soil data and field survey and the following values were used:  R = 160, K for the following soils Slidel and Topsey K=0.32, Brackett K=0.17,  C for the upper part of the watershed was set to C=0.2 (20% cover) and for the central and lower part C=0.04 (60% cover)

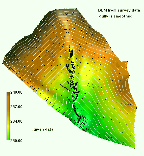
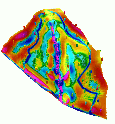
The Cs data were sampled at 100 points and erosion/deposition rates were derived using the models presented by Walling et al. 199?. ( see Warren et al., 1999). To visually compare the pattern of erosion and deposition derived from models and from the Cs data, we have interpolated the Cs-derived rates using RST (Figure 16)

Figure 16 Cs sampling points and interpolated spatial pattern

We have computed the maps of erosion and erosion/deposition using all the USLE methods described in section 2.2.1 and 2.3.1 with the results presented in Figure 16 a, b, c. By definition, the results do not show any deposition thus overestimating the spatial extent of erosion. The methods based on slope length predict the lowest erosion rates in the area where the erosion rates are the highest and gully is present. This demonstrates that when using slope-length approach the areas of concentrated flow should be identified (manually, from imagery or using flowtracing GIS tools) and modeled separately and the estimates added to the total and average soil loss. Such an approach would be extremely time consuming for large areas typical for military installations. The method based on the upslope area predicts the highest erosion rates in the center of the valley where the gully is located, however, it does not predict the deposition so the total erosion is overestimated.
Comparison with Cs data shows the missing deposition in the USLE results (Figure 9), however the values were the closest to the averaged slope length model - these results predicted relatively homogeneous distribution of erosion rates similar to the Cs distribution and also has very little relation with the amount of flowing water.

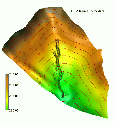
We have tested the USPED model for various values of m,n parameters (Figure 10). The model predicts both erosion and deposition, approximately in the areas indicated by the Cs measurements. However, the pattern from the USPED is more complex than the pattern derived from the Cs data (partially due to the fact that Cs was sampled by 100 points while the terrain was sampled by over thousand points) and the erosion rates predicted by USPED in the gully are substantially higher than the erosion rates on the ridges, while the Cs estimates in these areas are about the same. We have found that the lowest differences between the Cs and USPED were for the m=0.6 while the spatial extent of deposition was closest for m=1 (Table 1). This indicates impact of relatively local processes (in case of water erosion, short events with little runoff) which is in agreement with the published Cs research results.

erosion [%area] deposition [%area]
Cs137 72 28
p=0.6 56 41
p=1.0 74 25
p=1.6 81 18

Table 1. Spatial extent [%area] of erosion and deposition computed from the Cs measurements and USPED with different exponents

We have also computed an average from model results with m=0.6, 1.0, 1.6 approximating an impact of combination of smaller and larger events and prevailing sheet and rill erosion. The resulting estimate was relatively close to the Cs distribution and at the same time the pattern captured the gully erosion in the valley center. This indicates that it may be important to use continuous time simulations which capture the changes in rainfall and vegetation during the year, to predict the erosion/deposition pattern accurately.

Figure 17 Erosion deposition pattern averaged from both small and large events

The results show that calibration of water erosion models based on Cs is problematic and our experience from this project as well as several studies demonstrate that only a portion of the Cs movement can be explained by water erosion and that relatively local processes have a substantial impact in Cs distribution. For example, in agricultural areas, tillage erosion which which is not present in our area, is used to explain the Cs distribution (Quinne et al. 1998). Even more intriguing is the fact that Cs is bound to clay particles which can be carried by water over long distances and deposited into the lakes and rivers, so at least theoretically, the pattern of clay particle movement has a long range character as opposed to local character of Cs distribution.

SIMWE simulations were ran with the IFSARE data and will be run for the more accurate field data and reported in the future. The SIMWE model will allow us to explore the effects which are not captured in the USLE or USPED such as adding detachment by raindrops which is dependent from water flow (although the term seems to be relatively low) or diffusive term reflecting combined impact of various processes (weathering, wind, raindrop splash) which may be important  for long term effects.

A complete set of maps computed from both the IFSARE and the NRCS field data is available in online Appendix 1.4.1 and Appendix 1.4.2.
 

3.2 Fort Polk

The modeling at Fort Polk has been focused on creating a new digital elevation model as a basis for erosion simulations and performing modeling with the data that were available. Because the processing of Fort Polk DEM was performed as a separate contract, we describe it only briefly here to provide information about the procedure which was used. Computation of the DEM was a challenge because of the large volume of data and the size of the resulting grid. We were provided with the measured point elevation data and the contours derived from these data. Using a subset of the data we have compared the DEM computed a) from the point data, b) from the contour data c) from the combination of both. The comparison has shown that while the combination of point and contour data was computationally very demanding, the increase in accuracy compared to using just the one data set justified the extra effort. We have computed two DEMs for the entire Fort Polk installation: