usle

developed with GRASS5.0

Modeling soil detachment with RUSLE 3d using GIS

Helena Mitasova, Lubos Mitas, University of Illinois at Urbana-Champaign

1. Method

Original USLE and RUSLE

The Universal Soil Loss Equation is an empirical equation designed for the computation of average soil loss in agricultural fields. This equation was developed for detachment capacity limited erosion in fields
with negligible curvature and no deposition and represents soil loss averaged over time and total area. The equation has the following form (Wischmeier and Smith 1978, Renard et al. 1991)

E = R K L S C P

where E [ton/(acre.year)] is the average soil loss, R [hundreds of ft.tonsf.in/acre.hr.year] (in SI: [MJ.mm/ha.hr.year ], R[SI]=17.02R[EU]) is the rainfall intensity factor, K [tons per acre per unit R] = [tons.acre.hr/hundreds.acre.ft.tonsf.in] is the soil factor, LS [dimensionless] is the topographic (length-slope) factor, C [dimensionless] is the cover factor and P[dimensionless] is the prevention practices factor. Various modifications of this equation are often applied to the estimation of soil loss using GIS (Warren et al. 1989).
Revised USLE - RUSLE uses the same empirical principles as USLE, however it includes numerous improvements, such as monthly factors, incorporation of the influence of profile convexity/concavity using segmentation of irregular slopes, improved empirical equations for the computation of LS factor (Foster and Wischmeier1974, Renard et al. 1991).

LS factor modified for complex terrain

To incorporate the impact of flow convergence, the hillslope length factor was replaced by upslope contributing area A (Moore and Burch 1996, Mitasova et al. 1995, 1996, Desmet and Govers 1996). The modified equation for computation of the LS factor in GIS in finite difference form for erosion in a grid cell representing a hillslope segment was derived by Desmet and Govers (1996). A simpler, continuous form of equation for computation of the LS factor at a point r=(x,y) on a hillslope, (Mitasova et. al. 1996) is

LS(r) = (m+1) [ A(r) / a₀]^m [ sin b(r) / b₀]ⁿ

where A[m] is upslope contributing area per unit contour width, b [deg] is the slope, m and n are parameters, and a₀ = 22.1m = 72.6ft is the length and b₀ = 0.09 = 9% = 5.16deg is the slope of the standard USLE plot. Impact of replacing the slope length by upslope area is illustrated in FIGURE 1 (Length-based LS,Upslope area based LS) which shows that the upslope area better reflects the impact of concentrated flow on increased erosion. It has been shown that the values of m=0.6, n=1.3 give results consistent with the RUSLE LS factor for slope lengths <100m and slope angles <14 deg (Moore and Wilson 1992), for slopes with negligible tangential curvature. Exponents m and n can be calibrated if the data are available for a specific prevailing type of flow and soil conditions.

Both the standard and modified equations can be properly applied only to areas experiencing net erosion. Depositional areas should be excluded from the study area because the model assumes that transport capacity exceeds detachment capacity everywhere and erosion and sediment transport is detachment capacity limited. Therefore, direct application of USLE/RUSLE to complex terrain within GIS is rather restricted. The results can also be interepreted as an extreme case with maximum spatial extent of erosion possible.

2. GIS implementation

2.1 GRASS GIS

Given data:

raster: elevation, K, C, (P)

constants: R=120, resolution=10

Computation

1. r.flow elevation dsout=flowacc

2. r.slope.aspect  elevation slope=slope

3. r.mapcalc

      lsfac=1.6*exp(flowacc*resolution/22.1,0.6)*exp(sin(slope)/0.09,1.3)

      soilloss=R*K*C*P*lsfac

4. Optional: create new colortable, reclass to erosion risk classes, run statistics...

2.2 ArcView-Spatial Analyst

Given data

grid: elevation, K, C, (P)

constant: R=120, resolution=10

Computation

1. select elevation

   under Analysis select DERIVE SLOPE

   give the new theme name slope

2. MAP CALCULATOR

    build an expression

    ([elevation].FlowDirection(FALSE)).FlowAccumulation(NIL)

    Evaluate

    give the new theme name  flowacc

    build an expression :

    
(([flowacc] * resolution/22.1).Pow(0.6))*(((([slope]*0.01745).Sin)/0.09).Pow(1.3))*1.6

    Evaluate

    give the new theme name lsfac

    build an expression

    R*[K]*[C]*[P]*[lsfac]

    Evaluate

    give the new theme name soilloss

4. Optional: create new colortable, reclass to erosion risk classes, run statistics...

2.3 ArcGIS 8.1, ArcMap


Given data 

grid: elevation, K, C, (P)

constant: R=120, resolution=10


Computation 

1. Enable Spatial Analyst
   
   under View... Toolbars  select Spatial Analyst

2. Calculate Slope

   from the Spatial Analyst toolbar, select Surface Analysis... Slope

   give the new theme name slope

3. Raster Calculator 

   from the Spatial Analyst toolbar, select Raster Calculator

   build an expression:
   
   FlowAccumulation(FlowDirection([elevation]))

   Evaluate
   
   make the new theme permanent and change the name to flowacc

   build an expression in the Raster Calculator:

   Pow([flowacc] * resolution / 22.1, 0.6) * Pow(Sin([slope] * 0.01745) / 0.09, 1.3))

   Evaluate

   make the new theme permanent and change the name to lsfac

   build an expression in the Raster Calculator:

   R*[K]*[C]*[P]*[lsfac]

   Evaluate

   make the new theme permanent and change the name to soilloss

2.4 Notes

The results greatly depend on the quality of input data. especially elevation - horizontal resolution higher than 30m and vertical resolution (precision) 1cm is recomended, although results for lower resolutions can be still useful for regional scale applications. Do not resample DEM by changing region - choose suitable interpolation .

Areas of concentrated flow have higher soil loss than what is usually published for USLE. USLE is not designed to predict soil loss from such areas, however, our experience shows that it is useful to include these areas because they reflect the realistic increase in erosion often with potential for formation of gullies. Their spatial extent is very small compared to other areas so their impact on e.g. average soil loss from the entire region is usually small. In case that the values are unrealistically high, it is recommended to reclass them a uniform value which would be typical for gully erosion in the study region.

3. Refrences and links to related sites

Mitasova, H., J. Hofierka, M. Zlocha, L.R. Iverson, 1996, Modeling topographic potential for erosion and deposition using GIS. Int. Journal of Geographical Information Science, 10(5), 629-641. (reply to a comment to this paper appears in 1997 in Int. Journal of Geographical Information Science, Vol. 11, No. 6)

Mitasova, H., Mitas, L., Brown, W. M., Johnston, D., 1998, Multidimensional Soil Erosion/deposition Modeling and visualization using GIS. Final report for USA CERL. University of Illinois, Urbana-Champaign, IL.

GIS, Erosion and Deposition Modelling, and Caesium Technique at University of Exeter, Geography Department
This site has a comprehensive list of links to erosion modeling websites

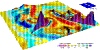Back to erosion

Spatial modeling and visualization team

Geographic modeling systems Lab
.