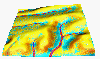
 r=36mm/h
r=36mm/h
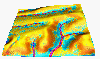 r=72mm/h
r=72mm/h
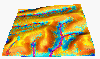 r=144mm/h
r=144mm/h

Lubos MITAS, Helena MITASOVA
University of Illinois at Urbana-Champaign
DRAFT
http://www.edv.agrar.tu-muenchen.de/fam/hello_fam.html
http://www.edv.agrar.tu-muenchen.de/fam/scheyern/ressource.html
http://www.cecer.army.mil/grass/viz/SF.final/mitas.html
add here illustrated computation with maps of: elevation,
direction of flow, slope, velocity (magn), water depth,
water discharge
shear stress, stream power, detachment capacity, transport capacity,
.....
(generalized 2D version of analysis presented by Wischmeier 1969 for profile) The base situation for all examples is 36mm/hour rainfall intesity, full saturation, rough surface (dense grass), sandy soil (negiligible critical shear stress, sigma=1, low detachability(erodibility) and transportability Kt=Kd=0.0003) Parameters are described in depth in the WEPP manual.
Rainfall excess (rainfall intensity - infiltration) influences the magnitude of erosion/deposition rates:
Surface roughness (represented by mannings n, chezy or darcy-weisbach) influences ration of spatial extent of erosion/deposition, the rougher the surface the greater the spatial extent of deposition
(keep Kt=Kd=konst, change only n)
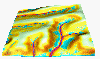
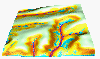
Critical shear stress (or critical stream power) has impact on ersoion/deposition pattern, its high value reduces the spatial extent of erosion, however it can increase the magnitude of erosion rates in steeper and/or convergent areas. (light green areas have no detachment=no erosion)
 tauc=1.
tauc=1.
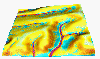 tauc=3.
tauc=3.
 tauc=5.
tauc=5.
 tauc=7.
tauc=7.
Erodibility (detachment capacity coefficient) Changes spatial distribution of erosion/deposition, does not change the magnitude of sediment load in stream
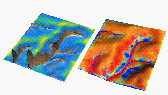 movie, Kd=(0.0001,0.1), Kt=0.001(oprav)
movie, Kd=(0.0001,0.1), Kt=0.001(oprav)
Transportability (transport capacity coefficient) Changes both spatial distribution and magnitude of sediment flow as well as erosion/deposition rates significantly.
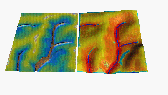 movie, Kt=(0.0001,0.1), Kd=0.001(oprav)
movie, Kt=(0.0001,0.1), Kd=0.001(oprav)
The parameters do not act independently, they are interrelated and it is the interaction which controls the pattern and magnitude of erosion. For example of both Kd and Kt change at the same rate, only magnitude of erosion/deposition changes and the spatial distribution stays the same. Illustration of a realistic change for the uniform case (WRR paper)
4.1Impact of differences between the properties
of two different covers and/or soils at different location within
a complex terrain using theoretical combinations of parameters.
rainfall excess (due to difference in infiltration)
roughness 0.1/0.05, 0.1/0.01
erodibility (detachment coef. Kd) 0.03/0.0003, 0.003/0.0003
transportability (Kt) 0.03/0.0003, 0.003/0.0003
sigma Kd/Kt
tauc
4.2 Observed and simulated erosion depposition for original
land use for:
a) small event and dense cover
b) large event and bare soil
Compare with colluvial deposits, linear erosion features, profiles(yields, Cs), density of rills-erosion potential
4.3Simulated water depth, sediment flow rate and net erosion/deposition for the orginal, new(sustainable) and computer designed land use, for the time of the year when the agricutural land (brown) is bare and grass cover(green) is well developed ( Table 1. Values of parameters used in this simulation).
Land cover Water Sediment flow Erosion/depositionA
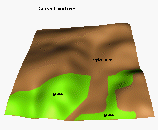




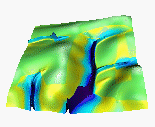


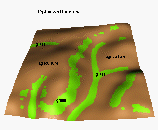
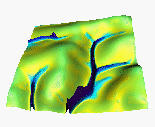

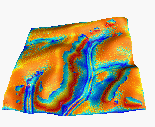
A : traditional land use (21% grass)
B : new sustainable land use (41% grass)
C : computer generated land use (19% grass)
Note: rerun water for B to reach steady state
Note the high erosion around buffers where the difference in Mannings is high ( add a different view)
Both B and C hold more water, reduce the max. sediment flow rates and max erosion rates. Note the proper simulation of deposition in the upper parts of grass areas, and increased erosion below the grass contour strips: phenomena which are difficult to model by more traditional methods.
1. n=0.01/0.1, Kt=Kd=0.03/0.0003
n=0.01/0.1, Kt=Kd=0.03/0.0003
2. 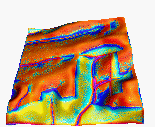 n=0.05/0.1, Kt=Kd=0.03/0.0003
n=0.05/0.1, Kt=Kd=0.03/0.0003
Note: when n changes, also Kt needs to be modified(?) to reflect
change in transportability for rougher surface? Explore changes only n -
surface is rougher but soil is as transportable as before. Change both
n and kt - increased cover cause increase in roughness and decrease
in transportability(?)
this allows us to evaluate the effectiveness of land use design under different cover conditions, as the vegetation develops over the year.
This work was partially supported by DOD Strategic Environmental Research and Development Program. ( SERDP).

 GMSL Modeling &
Visualization Home Page
GMSL Modeling &
Visualization Home Page
Helena Mitasova (GMSLab)
helena@gis.uiuc.edu Bill Brown (GMSLab)
brown@gis.uiuc.edu Lubos Mitas (NCSA)
lmitas@ncsa.uiuc.edu